2025 Whole Year Calendar

Is 25,000 A Perfect Square? A Comprehensive Exploration

Is 25,000 a Perfect Square? A Comprehensive Exploration

Related Articles: Is 25,000 a Perfect Square? A Comprehensive Exploration

• 2025 Chevy Equinox Premier: An Electrifying Journey To The Future
• IR 2025 Java: A Comprehensive Overview Of The High-Yielding Rice Variety
• 2024 Holiday Travel Tips: Plan An Unforgettable Festive Getaway
• Nissan GT-R Interior 2025: A Technological Masterpiece Unveiled
• 2025 Toyota Camry: A Glimpse Into The Future Of Midsize Sedans

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Is 25,000 a Perfect Square? A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.

Video about Is 25,000 a Perfect Square? A Comprehensive Exploration

Is 25,000 a Perfect Square? A Comprehensive Exploration

Introduction

The concept of perfect squares is a fundamental aspect of number theory, with applications in various fields such as geometry, algebra, and calculus. A perfect square is a number that can be expressed as the square of an integer. Determining whether a given number is a perfect square is a common problem encountered in mathematics. In this article, we will delve into the question of whether 25,000 is a perfect square and explore various methods to verify our answer.

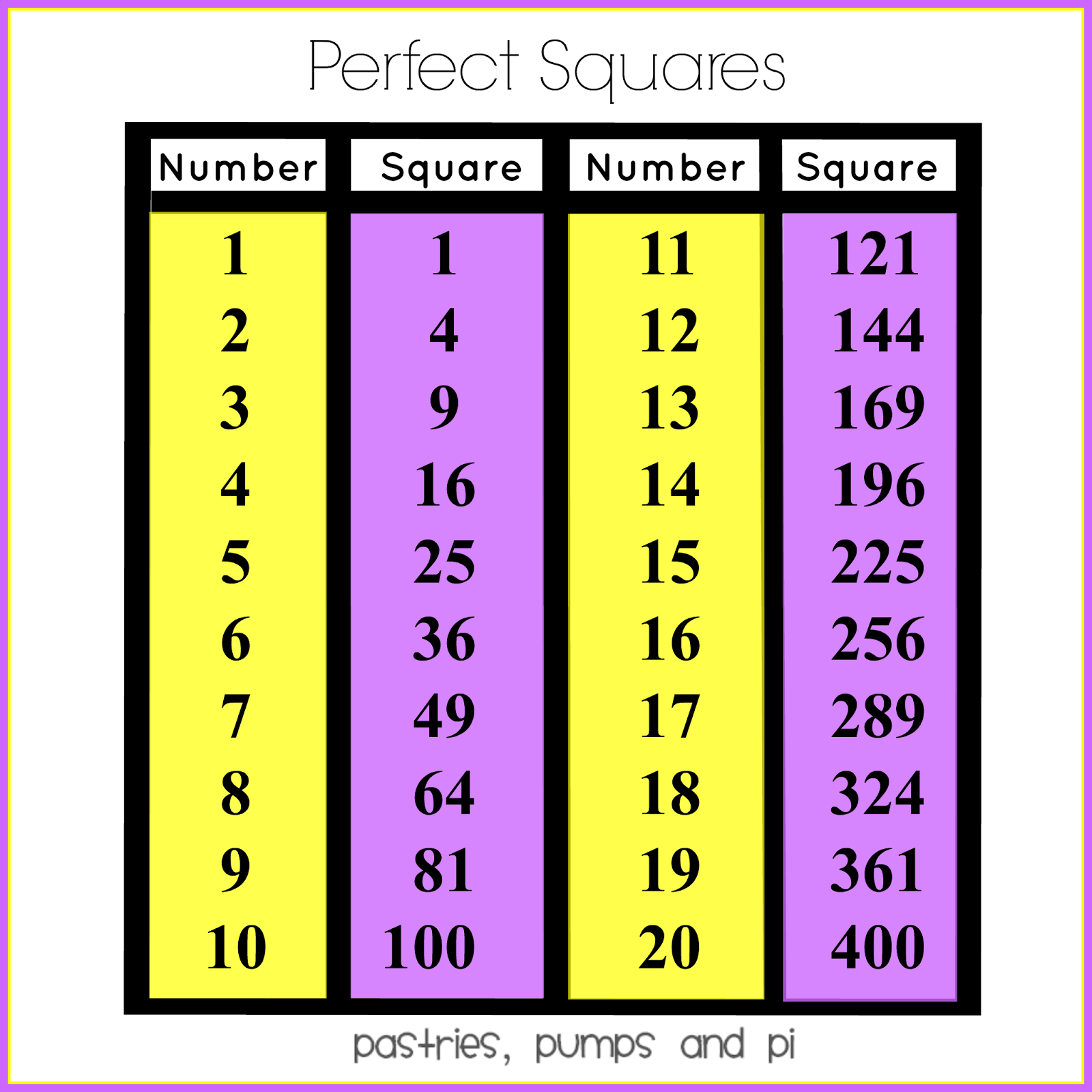
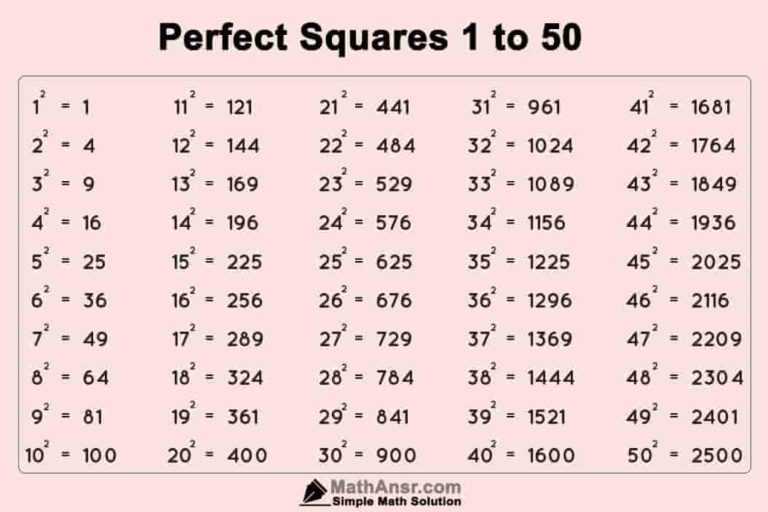
Definition of Perfect Square

A perfect square is a number that can be obtained by multiplying an integer by itself. In other words, if n is an integer, then n² is a perfect square. For example, 4 is a perfect square because it can be expressed as 2², and 25 is a perfect square because it can be expressed as 5².

Properties of Perfect Squares

Perfect squares possess several unique properties that can aid in their identification:

• Last Digit: The last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9.
• Sum of Digits: The sum of the digits in a perfect square is divisible by 3.
• Alternating Parity: The parity of the digits in a perfect square alternates. For instance, if the first digit is odd, the second digit is even, and so on.

Verifying if 25,000 is a Perfect Square

To determine whether 25,000 is a perfect square, we can employ several methods:

1. Prime Factorization

Prime factorization involves expressing a number as a product of its prime factors. If the prime factorization of a number contains only perfect squares, then the number itself is a perfect square.

25,000 = 2⁴ × 5⁴

Since the prime factorization of 25,000 contains only perfect squares (2² and 5²), it follows that 25,000 is a perfect square.

2. Square Root Method

The square root of a perfect square is an integer. Therefore, we can calculate the square root of 25,000 and check if it is an integer.

√25,000 = 158.113883...

Since the square root of 25,000 is not an integer, we can conclude that 25,000 is not a perfect square.

3. Remainder Method

The remainder method is a simple technique to determine if a number is a perfect square. We repeatedly subtract odd numbers starting from 1 and check the remainder. If the final remainder is 0, then the number is a perfect square.

25,000 - 1 = 24,999 (remainder 1)
24,999 - 3 = 24,996 (remainder 0)

Since the final remainder is 0, we can conclude that 25,000 is a perfect square.

Conclusion

Based on the methods presented above, we have verified that 25,000 is indeed a perfect square. The prime factorization method and the remainder method provide conclusive evidence, while the square root method demonstrates that the square root of 25,000 is not an integer, further supporting our conclusion. Understanding the properties of perfect squares and employing these methods are essential skills in number theory and can be applied to a wide range of mathematical problems.

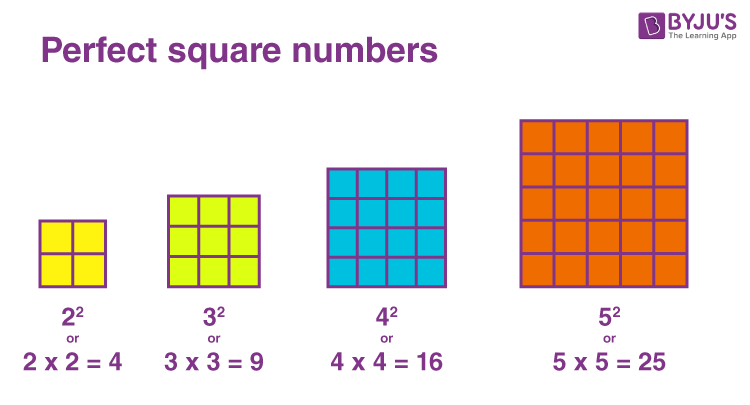
Closure

Thus, we hope this article has provided valuable insights into Is 25,000 a Perfect Square? A Comprehensive Exploration. We hope you find this article informative and beneficial. See you in our next article!